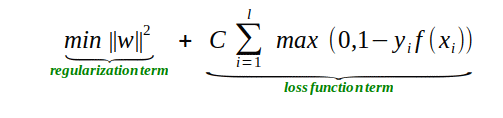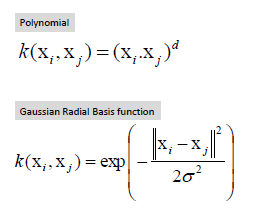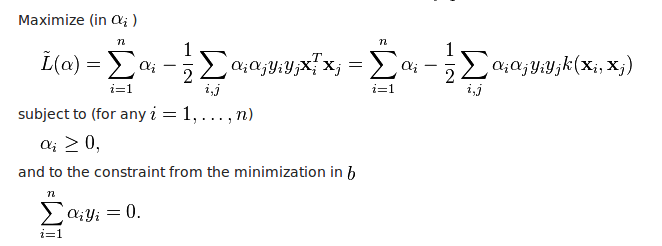SVM Sklearn In Python

Support Vector Machine is one of the classical machine learning algorithm.

It will solve the both Classification and Regression problem statements.

Before going deep down into the algorithm we need to undetstand some basic concepts

(i) Linaer & Non-Linear separable points

(ii) Hyperplane

(iii) Marginal distance

(iv) Support vector

SVM Basics

(i) Linear & Non-Linear Separable points

In [1]:
from IPython.display import Image
In [2]:
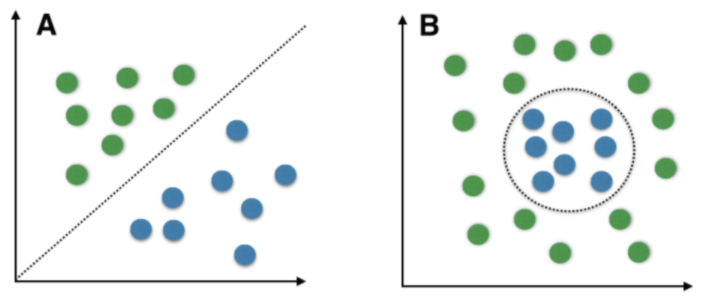
Image(filename='svm-classification.png',width = 600, height = 300)
Out[2]:

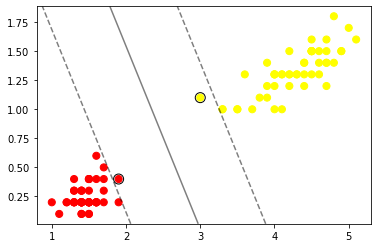
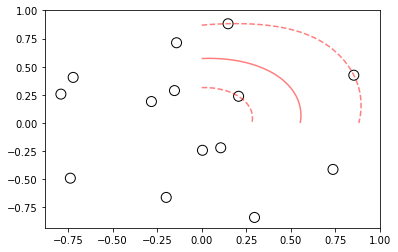
Linear separable points : If you obsereve the above fig A we have 2 class(green,blue) points.By using a line/hyperplane(3D) we can easily separtate these points.These type of points are called as linear separable points

Non-Linear separable points : If you observe the above fig B we have 2 class(green,blue) points we can't separate these points by using line/hyperplane(3D).These type of points are called as Non-Linear separable points.

Hyperplane

In [3]:
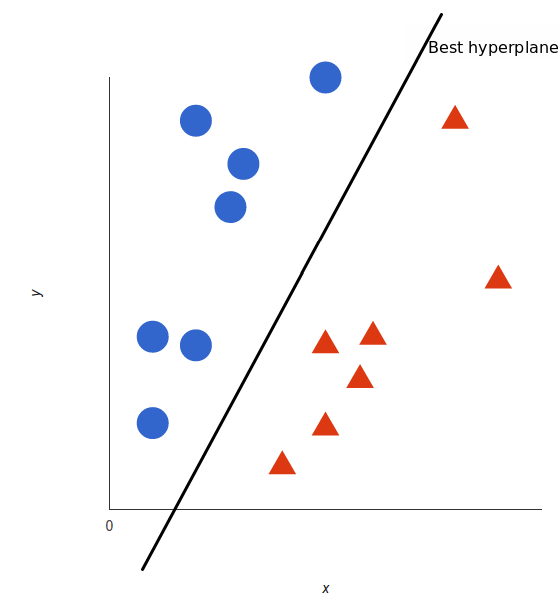
Image(filename="SVM_hyperplane.png",width = 400, height = 200)
Out[3]:

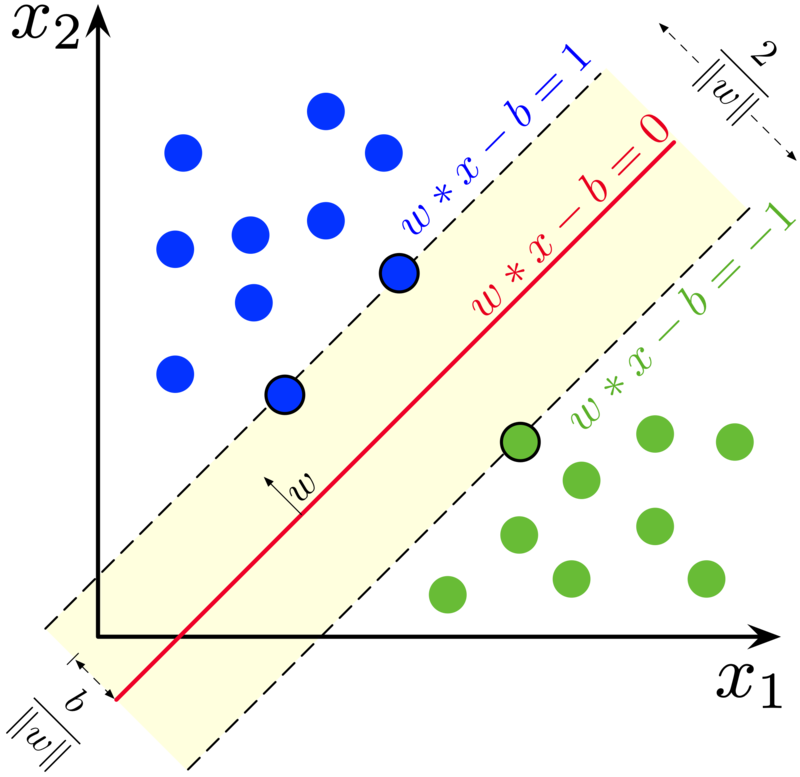
Hyperplane : The line/plane/hyperplane which separates the different class points

Marginal Distance

In [4]:
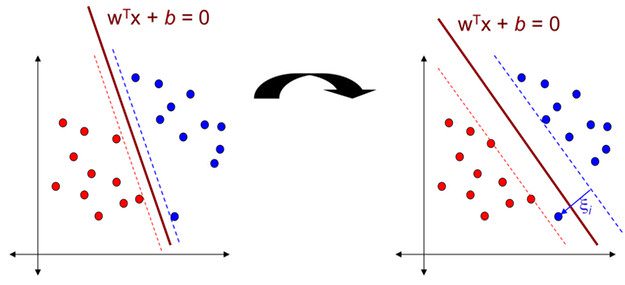
Image(filename="SVM_marginal_distance.png",width = 600, height = 300)
Out[4]:

If you observe the above two images the major differnece is the distance between dotted lines. The two dotted lines(blue,red dotted lines) are parallel to the hyperplane. If the distance between these two is large then there is less chance to be misclassification.

In SVM, the distance between these two dotted lines is called Margin.

Support Vectors

In [5]:
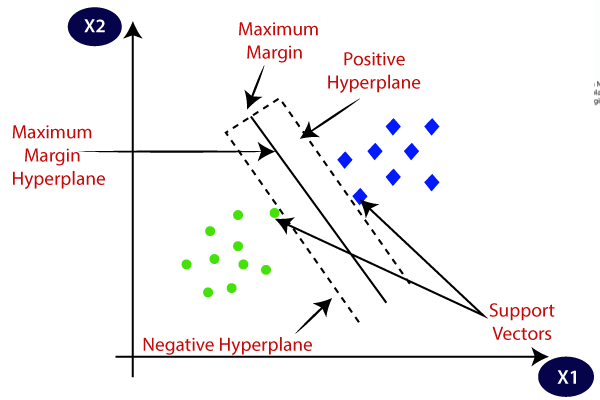
Image(filename="SVM_support_vectors.png",width = 600, height = 300)
Out[5]:

If you observe the above image the data points which passes through the dotted lines(both red,blue lines) are called as support vectors

These support vectors are very helpful to interpret the data point misclassified or not

The maximum distance is called margin

In linear speparable data the higher the marginal distance then our model more generalized model

The Objective is to make higher marginal distance so that we can easily separate the both the classes

Note : For Non-linear separable case svm doesn't give good results. That's why we us SVM Kernals for Non-linear case

SVM In A Nutshell

SVM : Support Vector Machine is a linear model for classification and regression problems. It can solve linear and non-linear problems and work well for many practical problems. The idea of SVM is simple, The algorithm creates a line or a hyperplane which separates the data into classes.

Objective of SVM is creating maximum marginal distance to build generalized model

How to find Marginal distance

In [6]:
Image(filename="svm_hyperplane_equation.png",width = 400, height = 200)
Out[6]:

Please checkout more about algorithm here

SVM Regularization and Loss Function

In [7]:
Image(filename="svm_regularization_lossfunction.png",width = 600, height = 300)
Out[7]:

Above equation is the objective function of SVM classification

In the equation we have two terms one is regularization term and another is loss term

In the loss term we have 'C', it's the hyperparameter trade-off is controlled by 'C'

C parameter adds a penalty for each misclassified data point. If c is small, the penalty for misclassified points is low so a decision boundary with a large margin is chosen at the expense of a greater number of misclassifications.

If c is large, SVM tries to minimize the number of misclassified examples due to high penalty which results in a decision boundary with a smaller margin. Penalty is not same for all misclassified examples. It is directly proportional to the distance to decision boundary.

Non-linear Separable Data

Upto now discussed things works for Linear separable data.

For Non-linear separable data we need to SVM Kernals

In [8]:
Image(filename="SVM_kernels.png",width = 600, height = 300)
Out[8]:

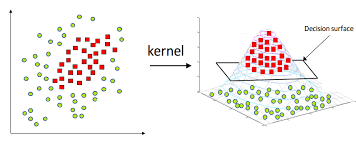
If you observe the above image data is Non-linear separable data. By using mariginal distance technique we can't separate the data points

For this case we use Kernals . Kernals is nothing but similarity(degree closeness) checking.

The working principle of kernal is transforming 2D data points into high dimensonality and then separate those points using plane/hyperplane

Most commonly used keranl function is Radia baisi function(RBF).

In [9]:
Image(filename="SVM_RBF_kernel.png")
Out[9]:

Kernal(RBF) svm objective function

In [10]:
Image(filename="SVM_RBF_objective_function.png")
Out[10]:

In RBF kernal funtion gamma is the hyperparameter. In Kernal SVM we need to optimize both C,gamma.

Gamma parameter of RBF controls the distance of influence of a single training point. Low values of gamma indicates a large similarity radius which results in more points being grouped together

For high values of gamma, the points need to be very close to each other in order to be considered in the same group (or class)

Note : For a linear kernel, we just need to optimize the c parameter. However, if we want to use an RBF kernel, both c and gamma parameter need to optimized simultaneously. If gamma is large, the effect of c becomes negligible. If gamma is small, c affects the model just like how it affects a linear model.

SVM Regression

SVM is also used for regression problems but most of the time SVM is used for classification problems.

SVM in Python On Real World Dataset

I am choosing familar dataset because here my objective is to explain SVM alogrithms and it's hyperparameters.

Linearly Separable Data :

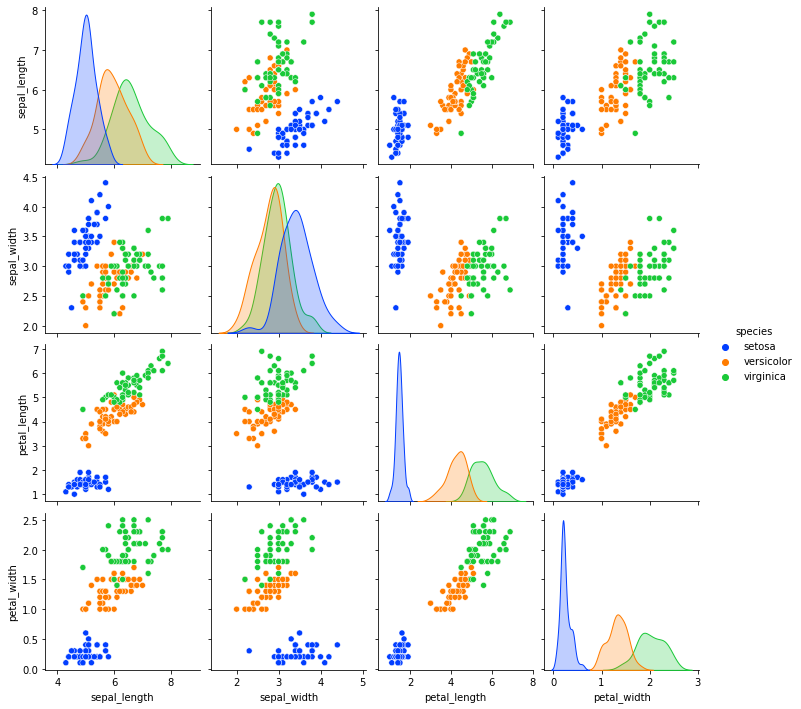
For this purpose, I’m going to use only two features and two classes of the Iris dataset (which contains 4 features and 3 classes). To do so, let’s first have a look at the correlation among features, so that we can pick features and classes which guarantee a linearly-separable data.

Correlation Using Seaborn Pairplot

In [1]:
# loading Iris data set

import seaborn as sns
iris = sns.load_dataset("iris")
print(iris.head())
y = iris.species
X = iris.drop('species',axis=1)
sns.pairplot(iris, hue="species",palette="bright")

   sepal_length  sepal_width  petal_length  petal_width species
0           5.1          3.5           1.4          0.2  setosa
1           4.9          3.0           1.4          0.2  setosa
2           4.7          3.2           1.3          0.2  setosa
3           4.6          3.1           1.5          0.2  setosa
4           5.0          3.6           1.4          0.2  setosa
Out[1]:
<seaborn.axisgrid.PairGrid at 0x7f87a372d2e8>

If you observe the above pair plots, petal_length and petal_width features are eaisly separable.

Let us drop sepal_length and sepal_width since we are focusing on petal_length and petal_width for now.

In [12]:
# I am keeping only 2 classes setosa ,versicolor and droppping others

import matplotlib.pyplot as plt

df=iris[(iris['species']!='virginica')]
df=df.drop(['sepal_length','sepal_width'], axis=1)
df.head()
Out[12]:
petal_length petal_width species
0 1.4 0.2 setosa
1 1.4 0.2 setosa
2 1.3 0.2 setosa
3 1.5 0.2 setosa
4 1.4 0.2 setosa

Let us convert categorical values to numerical values first.

In [13]:
# converting class names into numerical forms 
# plot between setosa and versicolor

df=df.replace('setosa', 0)
df=df.replace('versicolor', 1)
X=df.iloc[:,0:2]
y=df['species']
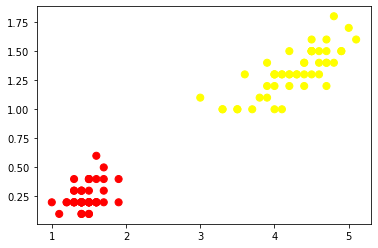
plt.scatter(X.iloc[:, 0], X.iloc[:, 1], c=y, s=50, cmap='autumn')
plt.show()

If you observe the above plot we can easily separate these two classes with line.

Train SVC on Linear Separable Data using Sklearn

In [14]:
from sklearn.svm import SVC 
model = SVC(kernel='linear')
model.fit(X, y)
Out[14]:
SVC(kernel='linear')

Coordianates of support vectors

In [15]:
model.support_vectors_
Out[15]:
array([[1.9, 0.4],
       [3. , 1.1]])

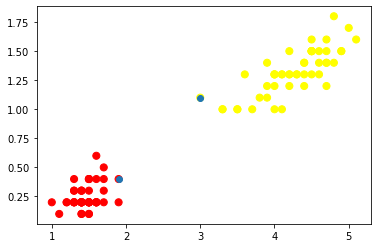
Visualize the SVM support vectors.

In [16]:
plt.scatter(X.iloc[:, 0], X.iloc[:, 1], c=y, s=50, cmap='autumn')
plt.scatter(model.support_vectors_[:,0],model.support_vectors_[:,1])
plt.show()

If you observe the above scatter plot, the blue color points are support vectors.

In [17]:
# Now visualizing the mariginal distance and hyperplane 
import numpy as np


ax = plt.gca()
plt.scatter(X.iloc[:, 0], X.iloc[:, 1], c=y, s=50, cmap='autumn')
xlim = ax.get_xlim()
ylim = ax.get_ylim()

xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = model.decision_function(xy).reshape(XX.shape)

ax.contour(XX, YY, Z, colors='k', levels=[-1, 0, 1], alpha=0.5,
           linestyles=['--', '-', '--'])

ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=100,
           linewidth=1, facecolors='none', edgecolors='k')
plt.show()

If you observe the above scatter plot we have hyperplane and marginal distance dotted lines.

SVM Model Train Without Hyperparameter Tuning Using Sklearn

In [18]:
# data frame 
iris.head()
Out[18]:
sepal_length sepal_width petal_length petal_width species
0 5.1 3.5 1.4 0.2 setosa
1 4.9 3.0 1.4 0.2 setosa
2 4.7 3.2 1.3 0.2 setosa
3 4.6 3.1 1.5 0.2 setosa
4 5.0 3.6 1.4 0.2 setosa

Let us convert Categorical features into numerical features first.

In [19]:
iris['species']=iris['species'].replace('setosa',0)
iris['species']=iris['species'].replace('virginica',1)
iris['species']=iris['species'].replace('versicolor',2)
In [20]:
# dividing  independent and dependent features 
X= iris.iloc[:,:-1]
y= iris.iloc[:,-1]

Let us Split the dataframe into train and test data using Sklearn.

In [21]:
from sklearn.model_selection import train_test_split 
  
X_train, X_test, y_train, y_test = train_test_split( X,y,  test_size = 0.30, random_state = 101)
In [22]:
# importing metrics 

from sklearn.metrics import classification_report

Model fitting to the train data set using Sklearn SVC()

In [23]:
model = SVC() 
model.fit(X_train, y_train) 
  
# model prediction results on test data 

predictions = model.predict(X_test) 
print(classification_report(y_test, predictions)) 

              precision    recall  f1-score   support

           0       1.00      1.00      1.00        13
           1       0.92      1.00      0.96        12
           2       1.00      0.95      0.97        20

    accuracy                           0.98        45
   macro avg       0.97      0.98      0.98        45
weighted avg       0.98      0.98      0.98        45

If you observe the classification report without hyperparameter tuning, we are getting accuracy 98% and f1 score values for Class 0 is 100% , for class 1 is 96% and for class 2 is 97%.

we are taking small data set so we are getting good values but what about complex data sets . When we have complex data sets, we don't get good metric values until we tune the hyperparameters of SVM algorithm.

In the SVM 'C' & gamma are hyperparameters . we can find best hyperparameters using GridSearchCV and RandomizedSearchCV.

Find Hypertune Parameters Using GridSearchCV

GridsearchCV checks the all possibilites in the given hyperparameter values space.

In [24]:
%%capture
from sklearn.model_selection import GridSearchCV 
from sklearn.svm import SVC 
  
# defining parameter range 
param_grid = {'C': [0.1, 1, 10, 100, 1000],  
              'gamma': [1, 0.1, 0.01, 0.001, 0.0001], 
              'kernel': ['rbf','linear']}  
  
grid = GridSearchCV(SVC(), param_grid, refit = True, verbose = 3) 
  
# fitting the model for grid search 
grid.fit(X_train, y_train)
In [25]:
# best parameters by GridsearchCV
print(grid.best_params_) 

{'C': 1, 'gamma': 1, 'kernel': 'linear'}
In [26]:
# best estimatior 
print(grid.best_estimator_) 

SVC(C=1, gamma=1, kernel='linear')

Now let us predict the test values using the hyper parameters from GridsearchCV.

In [27]:
grid_predictions = grid.predict(X_test)
In [28]:
print(classification_report(y_test, grid_predictions)) 

              precision    recall  f1-score   support

           0       1.00      1.00      1.00        13
           1       1.00      1.00      1.00        12
           2       1.00      1.00      1.00        20

    accuracy                           1.00        45
   macro avg       1.00      1.00      1.00        45
weighted avg       1.00      1.00      1.00        45

If you observe the above classification_report accuracy is 100% and f1 score for all three classes is also 100% . This is very small data set that's the reason we are getting the perfect results.

Bottom line is that tuning Hypertuning parameters improve the model substantially.

SVM Sklearn on Non Linear Separable Data

For this example, I am creating my own sample of Non linear separable dataset as shown below.

In [29]:
# creating non linear dataset samples

from sklearn.datasets import make_circles

X,y = make_circles(n_samples=100, factor=.1, noise=.1)

Let us visualize our non linear data first using a scatter plot.

In [30]:
import matplotlib.pyplot as plt
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
Out[30]:
<matplotlib.collections.PathCollection at 0x7f2f3a62fc18>

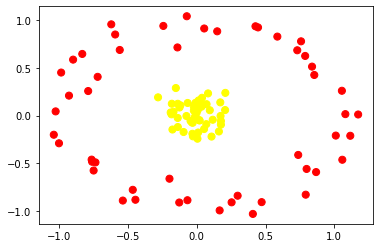
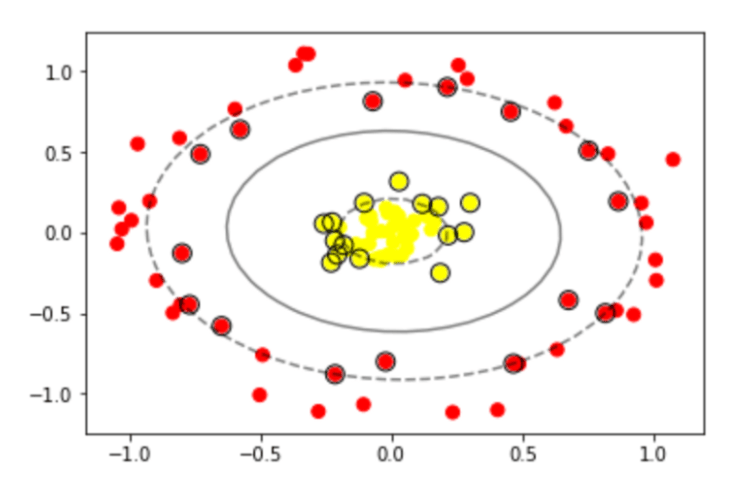
If you observe the above scatter plot we can't separate two classes with line.

To solve above problem statement we are using SVM kernal

SVM kernal: transform the points into higer dimensions and then we can easily separate these points using a hyperplane.

SVM Train Data Using Linear Kernel

In [31]:
# trying linear svm on non-linear separable data 

model=SVC(kernel='linear').fit(X, y)

ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# create grid to evaluate model
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = model.decision_function(xy).reshape(XX.shape)
# plot decision boundary and margins
ax.contour(XX, YY, Z, colors='r', levels=[-1, 0, 1], alpha=0.5,
           linestyles=['--', '-', '--'])
# plot support vectors
ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=100,
           linewidth=1, facecolors='none', edgecolors='k')
plt.show()

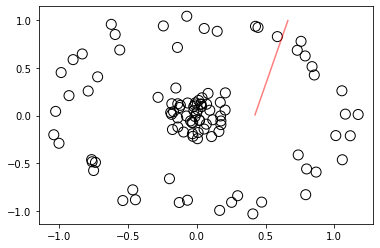
If you observe the above scatter plot, inner circular points (yellow color points in the previous scatter plot) and outer circlar points(red color circular points in the previous scatter plot) are not separated as efficently as we saw in the linear separable data set example above.

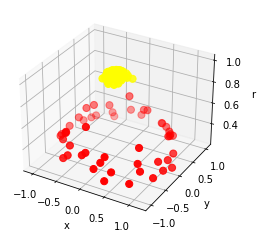
Ok, Let us visualize our data in 3D space using numpy and mplot3d.

In [32]:
#  converting non linear separable data from 2D to 3D


from mpl_toolkits import mplot3d
#setting the 3rd dimension with RBF centered on the middle clump
r = np.exp(-(X ** 2).sum(1))
ax = plt.subplot(projection='3d')
ax.scatter3D(X[:, 0], X[:, 1], r, c=y, s=50, cmap='autumn')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('r')
Out[32]:
Text(0.5, 0, 'r')

If you observe, in the above scatter plot, both the red and yellow color points are easily separable using plane/hyperplane.

we don't need to convert these non linear separable data into 3 dim because SVM kernal take cares of that.

SVM Train Data Using RBF Kernel

In [33]:
# Fiiting the train data SVM kernal . For nan linear separable data I am using RBF kernal

model=SVC(kernel='rbf').fit(X, y)
In [34]:
# visualizing the hyperplane and marginal distance in non linear separable data 

ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
# create grid to evaluate model
xx = np.linspace(xlim[0], xlim[1], 30)
yy = np.linspace(ylim[0], ylim[1], 30)
YY, XX = np.meshgrid(yy, xx)
xy = np.vstack([XX.ravel(), YY.ravel()]).T
Z = model.decision_function(xy).reshape(XX.shape)
# plot decision boundary and margins
ax.contour(XX, YY, Z, colors='r', levels=[-1, 0, 1], alpha=0.5,
           linestyles=['--', '-', '--'])
# plot support vectors
ax.scatter(model.support_vectors_[:, 0], model.support_vectors_[:, 1], s=100,
           linewidth=1, facecolors='None', edgecolors='k')
plt.show()
In [35]:
Image(filename="svm_nonlinear_decision_boundary.png",width = 400, height = 200)
Out[35]:

If you observe the above scatter plot, we have 1 hyperplane between inner and outer circular points.

Also have higher marginal distance

Conclusion

  • SVM is Simple and effective.
  • It can solve linear and non linear problems.
  • Try for linear separable data - linear kernel and for Non-linear separable data - rbf kernel(most commonly used kernel).
  • Try tuning Hyperparameters using range: 0.0001 < gamma < 10 and 0.1 < c < 100
  • No need to worry about feature engineering or feature transformtion because SVM can take care of it by Kernels.
  • SVM is less impacted by outliers.
  • Interpretability is not easy in SVM because interpreting kernels is very hard.
  • SVM is not for doing feature selection.
  • For Higher dimensional data, SVM works very well if we choose an appropriate kernal for classification.

Related Notebooks