Learn And Code Confusion Matrix With Python

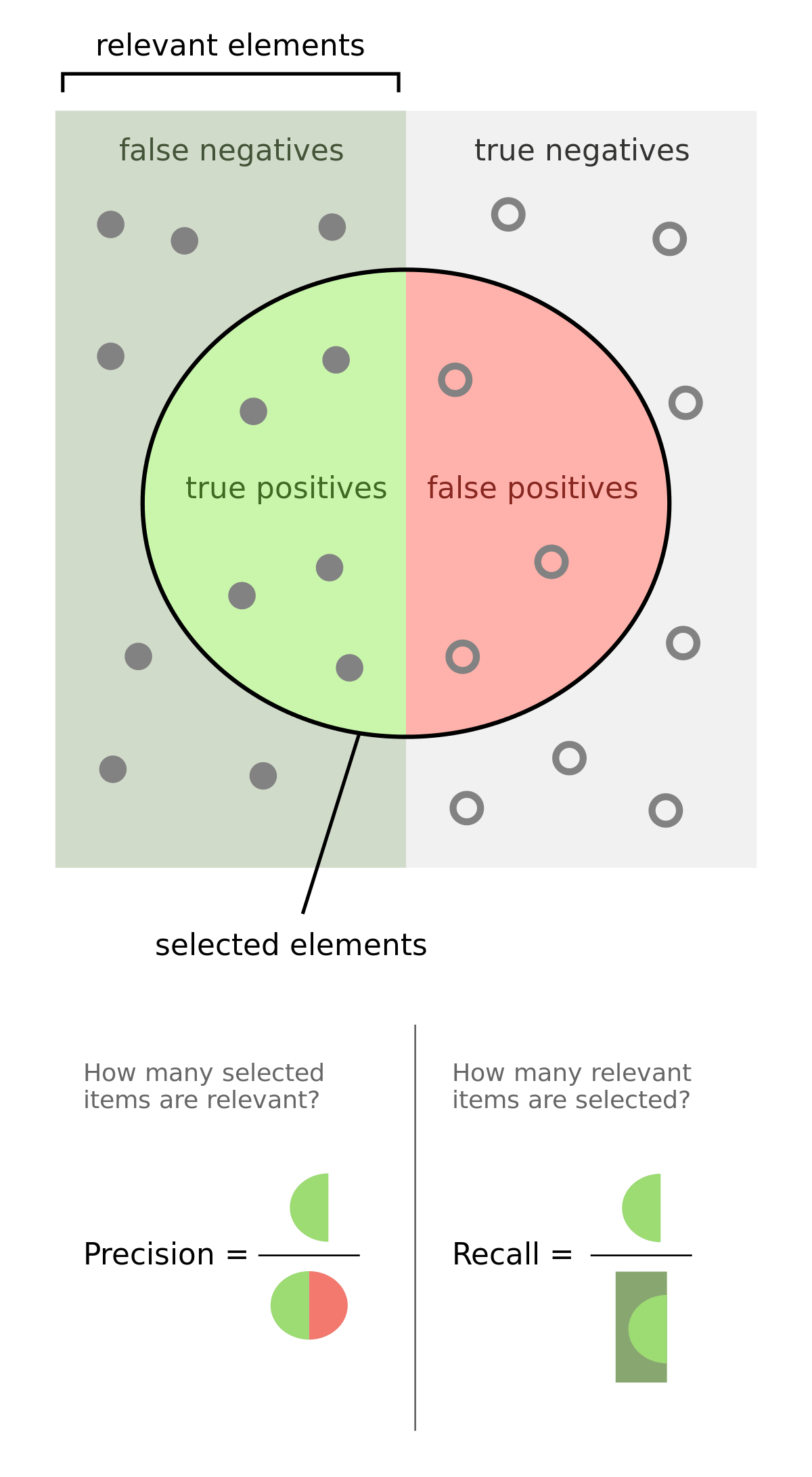
The confusion matrix is a way to visualize how many samples from each label got predicted correctly. The beauty of the confusion matrix is that it actually allows us to see where the model fails and where the model succeeds, especially when the labels are imbalanced. In other words, we are able to see beyond the model's accuracy.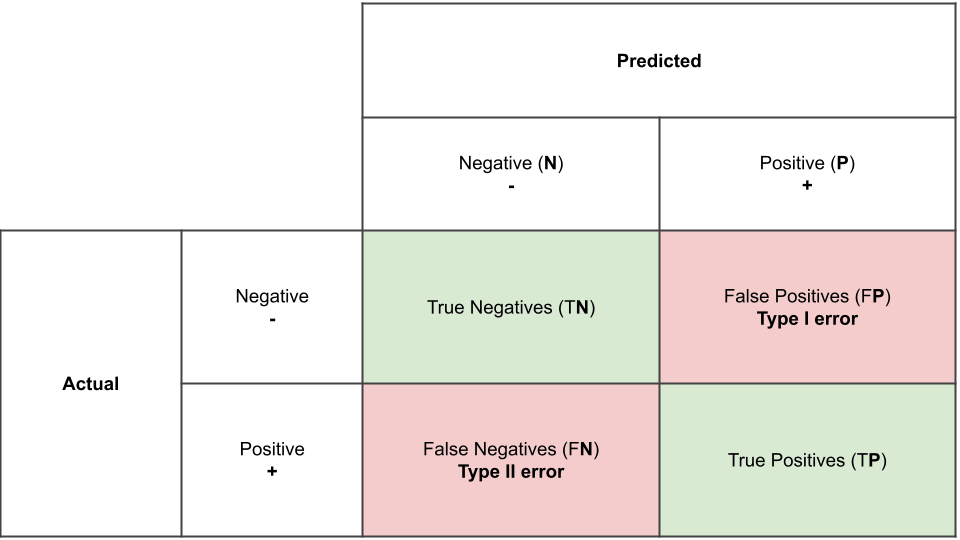

P.S. some people use predicted values on the rows, and actual values on the columns, which is just the transpose of this matrix. Some people start by the negative class first then the positive class. These are just different ways of drawing the confusion matrix, and all convey the same thing.

False Positives (FP-Type 1 error) vs False Negatives (FN-Type 2 error)

source

Confusion Matrix in Python

Let's try generating a confusion matrix in python

In [1]:
import random
import numpy as np
In [4]:
# first 50 values are positive-labels (1), second 50 values are negative-labels (0)
actual_values = [1] * 50 + [0] * 50
predicted_values = random.choices([0, 1], k=100) # randomly generate 0 and 1 labels
predicted_values[0:5]
Out[4]:
[1, 1, 0, 1, 1]

We can calculate then each of the 4 possible outcomes in the confusion matrix by simply comparing each value in the actual_values to its corresponding value in the predicted_values

In [5]:
fp = 0
fn = 0

tp = 0
tn = 0

for actual_value, predicted_value in zip(actual_values, predicted_values):
    # let's first see if it's a true (t) or false prediction (f)
    if predicted_value == actual_value: # t?
        if predicted_value == 1: # tp
            tp += 1
        else: # tn
            tn += 1
    else: # f?
        if predicted_value == 1: # fp
            fp += 1
        else: # fn
            fn += 1
            
our_confusion_matrix = [
    [tn, fp],
    [fn, tp]
]
# we convert it to numpy array to be printed properly as a matrix

our_confusion_matrix = np.array(our_confusion_matrix)
our_confusion_matrix
Out[5]:
array([[24, 26],
       [24, 26]])

We can get the same confusion matrix using sklearn.metrics.confusion_matrix function

In [6]:
from sklearn.metrics import confusion_matrix
In [7]:
confusion_matrix(actual_values, predicted_values)
Out[7]:
array([[24, 26],
       [24, 26]])

Accuracy

How many values did we predict correctly? How many true predictions out of all samples there are?

In [6]:
accuracy = (tp + tn)/100
accuracy
Out[6]:
0.5
In [7]:
# or
from sklearn.metrics import accuracy_score
accuracy_score(actual_values, predicted_values)
Out[7]:
0.5

Precision vs Recall

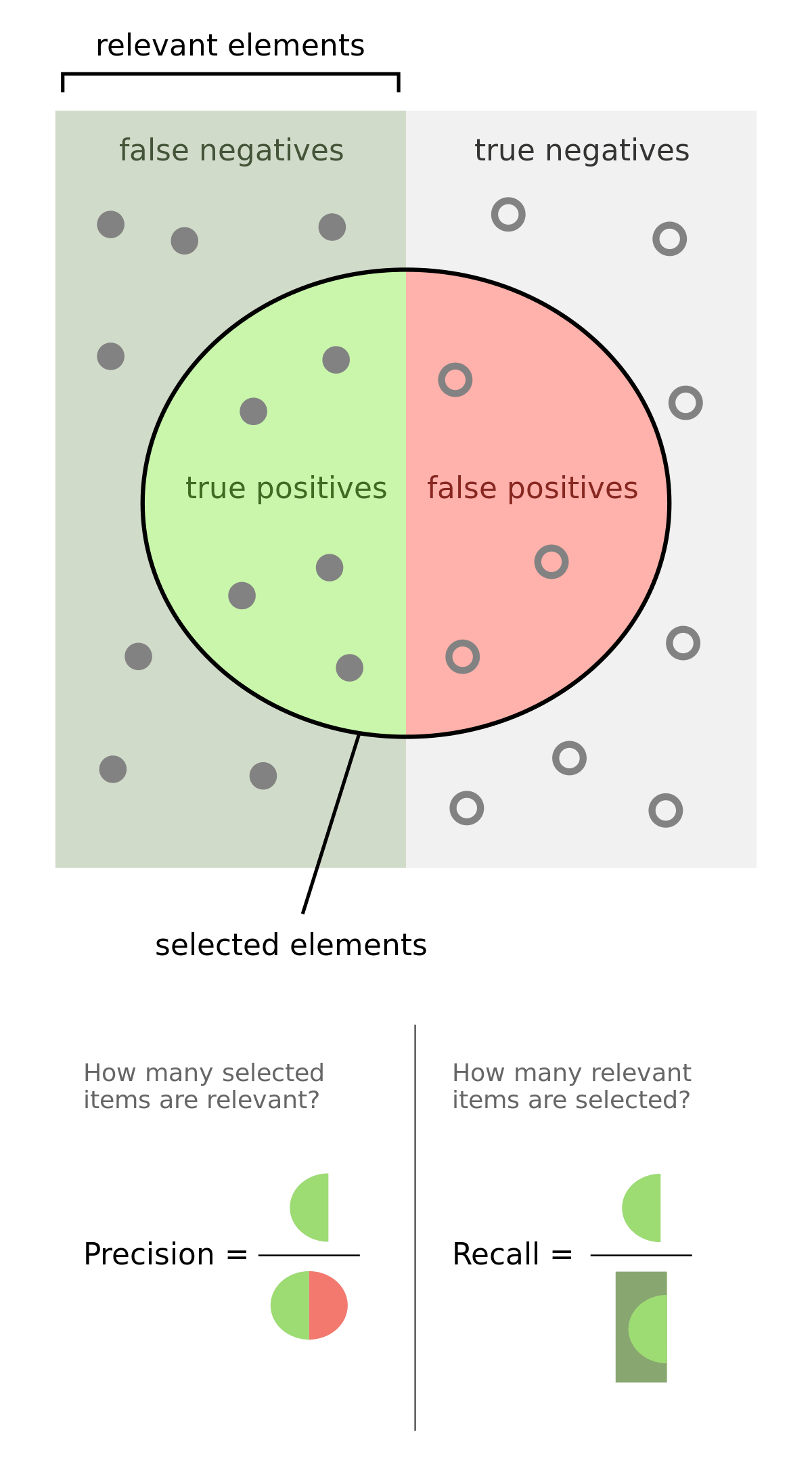
Precision

Precision calculates percentage of how many times a prediction is correct out of total predictions made. Example - If you predicted that 100 patients would catch Covid-19, but only 90 of patients actually got covid, then your precision is 90%. So out of all predicted positives (true positive and false positive) how many are actually true positive(tp)?

In [8]:
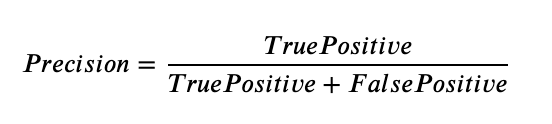
all_predicted_positives = tp+fp
precision_positive = tp / all_predicted_positives
precision_positive
Out[8]:
0.5
In [9]:
# or
from sklearn.metrics import precision_score
precision_score(actual_values, predicted_values, pos_label=1) # precision_positive
Out[9]:
0.5
In [10]:
# for the negative class
all_predicted_negatives = tn+fn
precision_negative = tn / all_predicted_negatives
precision_negative
Out[10]:
0.5
In [11]:
# here we trick sklearn to think that positive label is 0 not 1 :)
precision_score(actual_values, predicted_values, pos_label=0) # precision_negative
Out[11]:
0.5

Recall

Out of all actual positive samples, how many did you detect? For example, if there are 100 covid-19 patients, and in total you predicted only 50 of them as infected (positive), so your recall is 50%. So out of all actual positives (tp and fn), how many are predicted to be positive (tp).

In [12]:
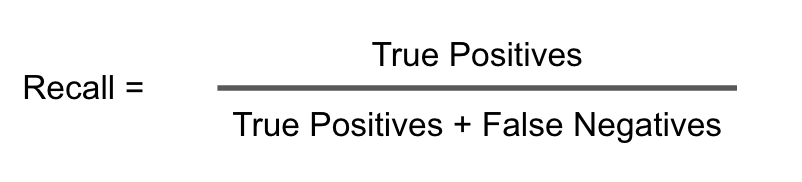
all_actual_positive = tp+fn
recall_positive = tp/all_actual_positive
recall_positive
Out[12]:
0.6
In [13]:
# or
from sklearn.metrics import recall_score
recall_score(actual_values, predicted_values) # recall_positive
Out[13]:
0.6
In [14]:
all_actual_negative = tn+fp
recall_negative = tn/all_actual_negative
recall_negative
Out[14]:
0.4
In [15]:
# here we trick sklearn to think that positive label is 0 not 1 :)
recall_score(actual_values, predicted_values, pos_label=0) # recall_negative
Out[15]:
0.4

Importance of Precision and Recall

Let's say your dataset has just 10 positive samples, and 90 negative samples. If you use a classifier that classifies everything as negative, its accuracy would be 90%, which is misleadingly. But the classifier is actually pretty dumb! So let's calculate the precision and recall for such a model

In [16]:
# data
actual_values = [0] * 90 + [1]*10
predicted_values = [0]*100

acc = accuracy_score(actual_values, predicted_values)

prec_pos = precision_score(actual_values, predicted_values)
recall_pos = recall_score(actual_values, predicted_values)

prec_neg = precision_score(actual_values, predicted_values, pos_label=0)
recall_neg = recall_score(actual_values, predicted_values, pos_label=0)

print(f"Accuracy: {acc}")
print(f"Precision (+): {prec_pos}")
print(f"Recall (+): {recall_pos}")

print(f"Precision (-): {prec_neg}")
print(f"Recall (-): {recall_neg}")

Accuracy: 0.9
Precision (+): 0.0
Recall (+): 0.0
Precision (-): 0.9
Recall (-): 1.0

/home/ammar/myenv/lib/python3.7/site-packages/sklearn/metrics/_classification.py:1272: UndefinedMetricWarning: Precision is ill-defined and being set to 0.0 due to no predicted samples. Use `zero_division` parameter to control this behavior.
  _warn_prf(average, modifier, msg_start, len(result))

Sklearn is warning us about a zero division? where is that. It is in the precision of the positive class. We should be dividing by all the predicited positives, but the model made no positive predictions, so that is a zero! More importantly, the positive recall is also zero, because the model did not detect any of the positive samples, as it is naively classifying everything as negative.

F1-score

In order to unify precision and recall into one measure, we take their harmonic mean, which is called F1-score

In [17]:
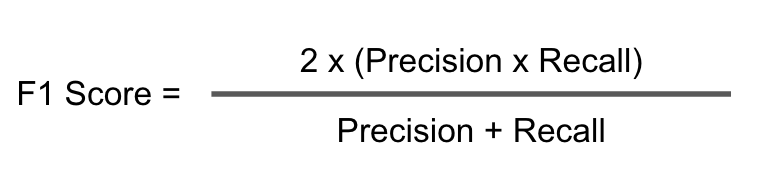
f1_positive = 2*(prec_pos * recall_pos)/(prec_pos+recall_pos)
f1_positive # nan because prec_pos is 0

/home/ammar/myenv/lib/python3.7/site-packages/ipykernel_launcher.py:1: RuntimeWarning: invalid value encountered in double_scalars
  """Entry point for launching an IPython kernel.
Out[17]:
nan
In [18]:
# or
from sklearn.metrics import f1_score
f1_score(actual_values, predicted_values) # sklearn handles this nan and converts it to 0
Out[18]:
0.0
In [19]:
f1_negative = 2*(prec_neg * recall_neg)/(prec_neg+recall_neg)
f1_negative
Out[19]:
0.9473684210526316

Sklearn Classification Reports

In sklearn you can show all of these results in one combined table! and also for more than two classes.

In [20]:
actual_values = [1]*30 + [2]*30 + [3]*30 + [4]*10 # 30 samples of each class 1,2, and 3 and 10 samples of class 4
predicted_values = random.choices([1,2,3,4], k=100) # 100 random samples
In [21]:
from sklearn.metrics import classification_report

print(classification_report(actual_values, predicted_values))

              precision    recall  f1-score   support

           1       0.39      0.23      0.29        30
           2       0.21      0.23      0.22        30
           3       0.32      0.23      0.27        30
           4       0.00      0.00      0.00        10

    accuracy                           0.21       100
   macro avg       0.23      0.17      0.19       100
weighted avg       0.27      0.21      0.23       100

Support: This columns tells you how many samples are in each class.

Macro Avg

For a multiclass classification problem, apart from the class-wise recall, precision, and f1 scores, we check the macro and weighted average recall, precision and f1 scores of the whole model. These scores help in choosing the best model for the task at hand.

In the above confusion matrix, if we do the average of precision column, we would get 0.23 as shown below. Similarly the averages of the other columns can be found out.

In [8]:
(0.39+0.21+0.32+0.00)/4.0
Out[8]:
0.22999999999999998

Weighted Avg

Weighted average is average of weighted score of each column. For Example Precision column weighted average score is calculated by multiplying the precision value with corresponding number of samples and then taking the average as shown below.

In [12]:
(0.39*30 + 0.21*30 + 0.32*30 + 0.00*10)/100
Out[12]:
0.276

Related Notebooks