Activation Functions In Artificial Neural Networks Part 2 Binary Classification

This is part 2 of the series on activation functions in artificial neural networks. Chek out part1 - how to use RELU in Artificial Neural Networks for building a Regression model.

In this notebook, I will talk about how to build a binary classification neural network model.

In [1]:
from collections import Counter

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import tensorflow as tf
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from tensorflow.keras.layers import Dense, Dropout, Input
from tensorflow.keras.models import Model

To ensure that every time we run the code we get the same results, we need following code so as to generate a fixed random seed.

In [ ]:
tf.random.set_seed(42)
np.random.seed(42)

Binary Classification

For this exercise, we will use breast cancer dataset which is available in sklearn datasets.

In [2]:
from sklearn.metrics import classification_report
In [3]:
from sklearn.datasets import load_breast_cancer
In [4]:
data = load_breast_cancer()
X = data["data"]
y = data["target"]
labels = data["target_names"]
In [5]:
X_train, X_test, y_train, y_test= train_test_split(X, y, random_state=42)
In [6]:
def annotate_bars(ax, patches, horizontal=False, as_int=True):
    for p in patches:
        if horizontal:
            w = p.get_width()
            w = int(w) if as_int else round(w, 3)
            if w == 0:
                continue
            ax.annotate(f"{w}", (p.get_width()* 1.01, p.get_y() +0.1), fontsize=14)
        else:
            h = p.get_height()
            h = int(h) if as_int else round(h, 3)
            if h == 0:
                continue
            ax.annotate(f"{h}", (p.get_x() +p.get_width()/2, p.get_height()* 1.01), fontsize=14)
    return ax
In [7]:
counter = Counter(y)
keys = counter.keys()
values = counter.values()
fig = plt.figure(figsize=(16, 9))
bar = plt.bar(keys, values)
annotate_bars(plt, bar.patches)
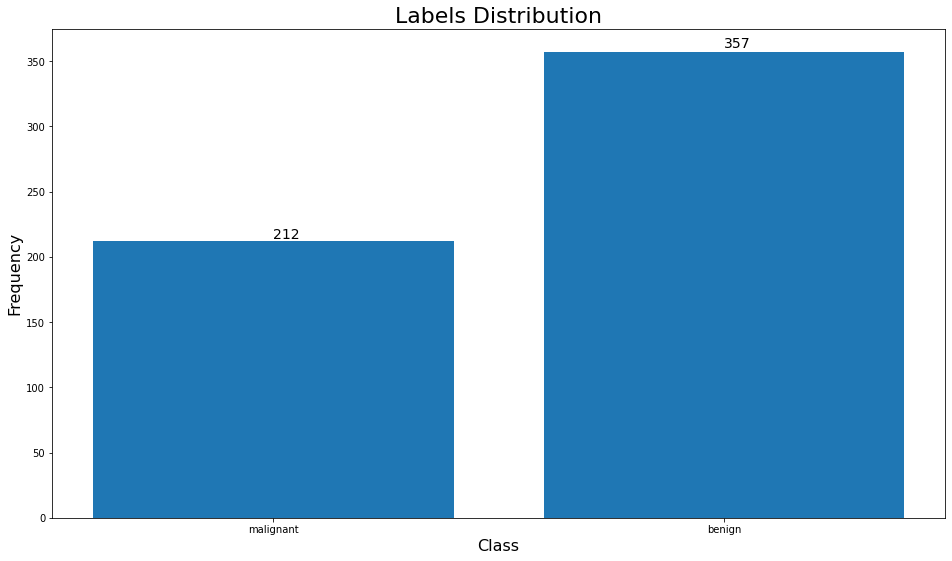
plt.xticks([0, 1], labels=["malignant", "benign"])
plt.xlabel("Class", fontsize=16)
plt.ylabel("Frequency", fontsize=16)
plt.title("Labels Distribution", fontsize=22)
plt.show()

We notice that the data is imbalanced, so we will need to do something about that before we train our model.

In [8]:
from sklearn.utils import compute_class_weight
In [9]:
class_weight = compute_class_weight('balanced', [0, 1], y_train)
class_weight
Out[9]:
array([1.34810127, 0.79477612])
In [10]:
class_weight_dict = dict(zip([0, 1], class_weight))
class_weight_dict
Out[10]:
{0: 1.3481012658227849, 1: 0.7947761194029851}

In the above code, we are giving higher weight to the under represented class 0 (i.e. malignant)

In [11]:
input_shape = X.shape[1] # number of features, which is 30

This is binary classification, So we only need one neuron to represent the probability of classifying the sample with the positive label.

In [ ]:
output_shape = 1

Activation Functions In Artificial Neural Network

Since this is a binary classification problem, we want the output to represent the probability of the selecting the positive class. In other words, we want the output to be between 0 and 1. A typical activation function for this is the *sigmoid* function. The sigmoid function is an example of the logistic function we use in logistic regression. It is an S-shaped curve that squashes the values to be between 0 and 1.

In [12]:
inputs = Input(shape=(input_shape,))
h = Dense(32, activation="relu")(inputs)
h = Dense(16, activation="relu")(h)
h = Dense(8, activation="relu")(h)
h = Dense(4, activation="relu")(h)
out = Dense(output_shape, activation="sigmoid")(h)
model = Model(inputs=inputs, outputs=[out])
model.summary()

Model: "functional_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_1 (InputLayer)         [(None, 30)]              0         
_________________________________________________________________
dense (Dense)                (None, 32)                992       
_________________________________________________________________
dense_1 (Dense)              (None, 16)                528       
_________________________________________________________________
dense_2 (Dense)              (None, 8)                 136       
_________________________________________________________________
dense_3 (Dense)              (None, 4)                 36        
_________________________________________________________________
dense_4 (Dense)              (None, 1)                 5         
=================================================================
Total params: 1,697
Trainable params: 1,697
Non-trainable params: 0
_________________________________________________________________

We use binarycrossentropy as the loss we want to minimize. This is the same one we have seen in logistic regression. $$-\frac{1}{n}\sum{i=1}^N{y_i\log(\hat{y_i})+(1-y_i)\log(1-\hat{y_i})}$$

In [13]:
model.compile(optimizer="adam", loss="binary_crossentropy", metrics="accuracy")
In [ ]:
H = model.fit(
    x=X_train,
    y=y_train,
    validation_data=(
        X_test, y_test
    ),
    class_weight=class_weight_dict,
    epochs=50,
)
In [15]:
f, axarr = plt.subplots(1,2, figsize=(16, 9))
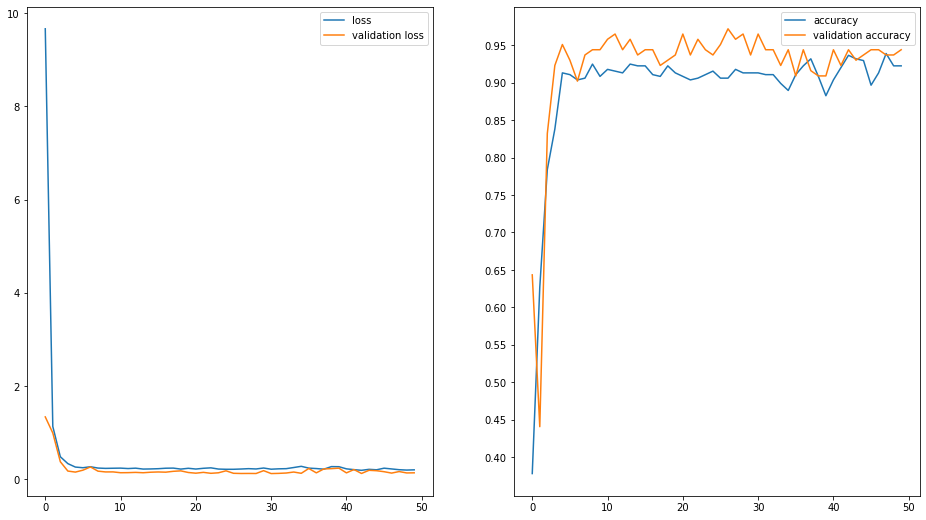
axarr[0].plot(H.history["loss"], label="loss")
axarr[0].plot(H.history["val_loss"], label="validation loss")
axarr[0].legend()

axarr[1].plot(H.history["accuracy"], label="accuracy")
axarr[1].plot(H.history["val_accuracy"], label="validation accuracy")
axarr[1].legend()
axarr[1].set_yticks(np.arange(0.4, 1, 0.05))
plt.show()

Let us now predict the probabilities.

In [16]:
pred_probs = model.predict(X_test) # predicted probabilities
y_pred=  pred_probs>=0.5 # higher than 50% probability means a positive class (i.e. class 1 or malignant)
print(classification_report(y_test, y_pred))

              precision    recall  f1-score   support

           0       0.90      0.96      0.93        54
           1       0.98      0.93      0.95        89

    accuracy                           0.94       143
   macro avg       0.94      0.95      0.94       143
weighted avg       0.95      0.94      0.94       143

Related Notebooks