Covid 19 Curve Fit Using Python Pandas And Numpy

In this post, We will go over covid 19 curve plotting for US states.

Before we delve in to our example, Let us first import the necessary package pandas.

In [6]:
import pandas as pd
from matplotlib import pyplot as plt
import numpy as np
In [7]:
df=pd.read_csv('covid19_us_states.csv',encoding='UTF-8')
In [8]:
df.head(2)
Out[8]:
date state fips cases deaths
0 1/21/2020 Washington 53 1 0
1 1/22/2020 Washington 53 1 0

Let us do a line plot for covid 19 cases of California.

In [9]:
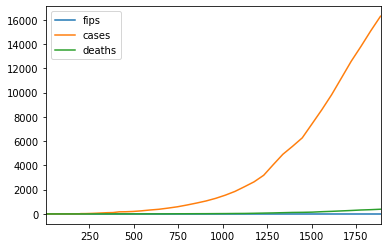
df[df.state=='California'].plot.line()
Out[9]:
<matplotlib.axes._subplots.AxesSubplot at 0x7ff080d237d0>

x axis in the above chart is the index number. To plot it against date, we need to set the index as date first.

Before that let us check what is the data type of date.

In [10]:
df.dtypes
Out[10]:
date      object
state     object
fips       int64
cases      int64
deaths     int64
dtype: object

We need to change date field from string to datetime using to_datetime() function.

In [11]:
df['date'] = pd.to_datetime(df['date'])
In [12]:
df.dtypes
Out[12]:
date      datetime64[ns]
state             object
fips               int64
cases              int64
deaths             int64
dtype: object

Ok date field is now datetime64 type. Let us now set the date as index.

In [13]:
dfd = df.set_index('date')

Let us try now plotting.

In [14]:
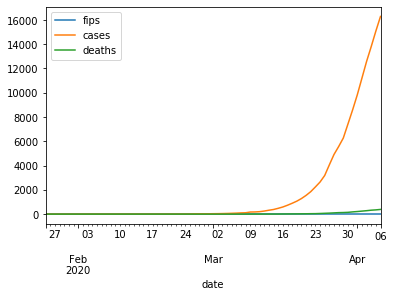
dfd[dfd.state=='California'].plot.line()
Out[14]:
<matplotlib.axes._subplots.AxesSubplot at 0x7ff07fe5c2d0>

As we can see above there were no cases of covid 19 before March 2020. Also note, the x-axis looks much better now. Let us filter out the data before March and replot.

In [15]:
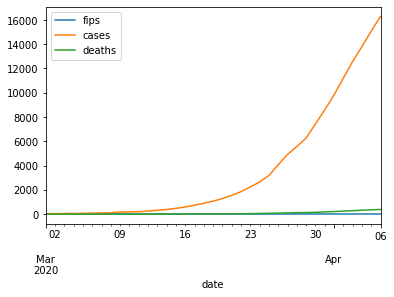
dfd[(dfd.state=='California') & (dfd.index >= '3/1/2020')].plot.line()
Out[15]:
<matplotlib.axes._subplots.AxesSubplot at 0x7ff07fa6fcd0>
In [16]:
dfd.head(2)
Out[16]:
state fips cases deaths
date
2020-01-21 Washington 53 1 0
2020-01-22 Washington 53 1 0

Compare covid 19 curve of California with New York

To compare the covid 19 cases of two states, we need to use subplots. We will compare the data beginning March 1 2020.

In [17]:
fig, ax = plt.subplots()
dff = dfd[dfd.index >= '2020-03-01']
dff[(dff.state=='California')]['cases'].plot(kind='line', ax=ax)
dff[(dff.state=='New York')]['cases'].plot(kind='line', ax=ax)
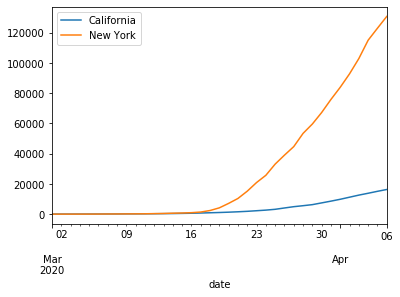
ax.legend(['California','New York'])
Out[17]:
<matplotlib.legend.Legend at 0x7ff07f6a0590>

The California curve looks much less steeper than New York curve for covid 19 cases.

Let us try to fit a curve to our data for New York covid 19 cases.

We will use numpy polyfit function to do that.

In [18]:
cases_newyork = dfd[dfd.state=='New York']['cases']

np.polyfit needs x-axis as numeric. It can't take date as it is.

Since date is an index, we can take number of date entries as x axis as shown below.

In [19]:
xaxis = range(len(dfd[dfd.state=='New York'].index))
In [20]:
xaxis
Out[20]:
range(0, 37)

Let us try fitting a 3 degree polynomial to our data.

In [21]:
coefficients = np.polyfit(xaxis,cases_newyork,3)
In [22]:
coefficients
Out[22]:
array([   3.39525731,    6.01871669, -887.61616607, 2684.08901412])

Let us build a polynomial using above coefficients. We need to import polynomial package using np.poly1d.

In [23]:
f = np.poly1d(coefficients)

Lets us print our polynomial equation now.

In [24]:
print(np.poly1d(coefficients))

       3         2
3.395 x + 6.019 x - 887.6 x + 2684

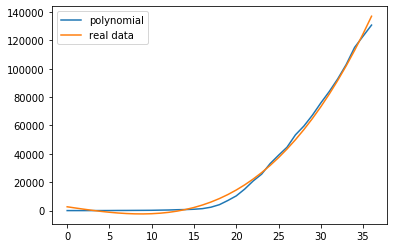
We will plot now our new york cases and then overlay our polynomial function on top of it.

In [25]:
fig, ax = plt.subplots()
plt.plot(xaxis, cases_newyork)
plt.plot(xaxis,f(xaxis))
ax.legend(['polynomial','real data'])
Out[25]:
<matplotlib.legend.Legend at 0x7ff07ac972d0>

As we see above the polynomial fits very well to our real data.

Let us try fitting our polynomial function to California covid 19 time series data.

In [26]:
cases_california = dfd[dfd.state=='California']['cases']
xaxis_california = range(len(dfd[dfd.state=='California'].index))
In [27]:
fig, ax = plt.subplots()
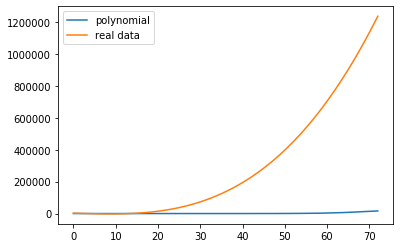
plt.plot(xaxis_california, cases_california)
plt.plot(xaxis_california,f(xaxis_california))
ax.legend(['polynomial','real data'])
Out[27]:
<matplotlib.legend.Legend at 0x7ff07ac59d10>

As we see above, the New York polynomial curve doesnt fit on the California covid 19 data.

Let us see which polynomial would best fit the California covid 19 data - checkout part 2 polynomial interpolation using sklearn.

Wrap Up!

I hope above examples would give you clear understanding about how to do curve fitting using Pandas and Numpy.

Related Notebooks